Gradient Descent Debug
April 9, 2019
关于梯度的调试
有时求解梯度会有困难,我们可以通过近似的方法来求解某点的梯度
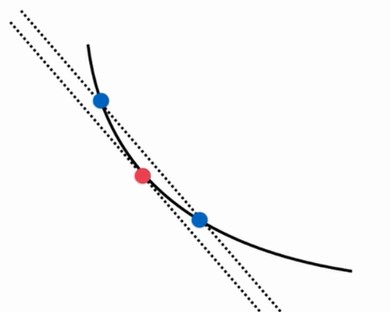
近似的计算导数
\[\frac{dJ}{d\theta} = \frac{J(\theta + \varepsilon) - J(\theta + \varepsilon)}{2\varepsilon}\]多维近似求梯度
\[\theta = (\theta_0, \theta_1, \theta_2, \ldots , \theta_n)\] \[\frac{\partial{J}}{\partial{\theta}} = (\frac{\partial{J}}{\partial{\theta_0}}, \frac{\partial{J}}{\partial{\theta_1}}, \frac{\partial{J}}{\partial{\theta_2}},\ldots, \frac{\partial{J}}{\partial{\theta_n}})\] \[\theta_0^+ = (\theta_0 + \varepsilon, \theta_1, \theta_2, \ldots , \theta_n)\] \[\theta_0^- = (\theta_0 - \varepsilon, \theta_1, \theta_2, \ldots , \theta_n)\] \[\frac{\partial{J}}{\partial{\theta_0}} = \frac{J(\theta_0^+) - J(\theta_0^-)}{2\varepsilon}\]其他维度同理
缺点:时间复杂度比较高
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.random(size=(1000, 10))
true_theta = np.arange(1,12, dtype=float)
X_b = np.hstack([np.ones((len(X), 1)), X])
y = X_b.dot(true_theta) + np.random.normal(size = 1000)
X.shape
(1000, 10)
y.shape
(1000,)
true_theta
array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.])
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
def dJ_math(theta, X_b, y):
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def dJ_debug(theta, X_b, y, epsilon=0.01):
res = np.empty(len(theta))
for i in range(len(theta)):
theta_1 = theta.copy()
theta_1[i] += epsilon
theta_2 = theta.copy()
theta_2[i] -= epsilon
res[i] = (J(theta_1, X_b, y) - J(theta_2, X_b, y)) / (2 * epsilon)
return res
def gradient_descent(dJ, x_b, y, initial_theta, eta, n_iters=10000, epsilon=1e-8):
theta = initial_theta
i_iter = 0
while i_iter < n_iters:
gradient = dJ(theta, x_b, y)
last_theta = theta
theta = theta - eta * gradient
i_iter = i_iter + 1
if(abs(J(theta, x_b, y) - J(last_theta, x_b, y)) < epsilon):
break
return theta
initial_theta = np.ones((X_b.shape[1]))
eta = 0.01
%time theta = gradient_descent(dJ_debug, X_b, y, initial_theta, eta)
theta
Wall time: 32 s
array([ 1.1200843 , 2.05379431, 2.91634229, 4.12015471, 5.05100799, 5.90580603, 6.97494716, 8.00169439, 8.86330612, 9.98697644, 10.90637129])
%time theta = gradient_descent(dJ_math, X_b, y, initial_theta, eta)
theta
Wall time: 4.44 s
array([ 1.1200843 , 2.05379431, 2.91634229, 4.12015471, 5.05100799, 5.90580603, 6.97494716, 8.00169439, 8.86330612, 9.98697644, 10.90637129])