<-- home

High Dimension To Low Dimension

April 13, 2019

高维数据映射为低维数据

高 —> 低

\[X_k = X \cdot W_k^T\]

其中 𝑋𝑘 为映射后的低维数据，X 为原始的高维数据， Wk 为前 k 个主成分

低 —> 高

\[X_m = X_k \cdot W_k\]

其中 𝑋m 为映射后的高维数据，Xk 为原始的高维数据映射后的低维数据， Wk 为前 k 个主成分，Xm 和原始 X 相比有损失

import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100,2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)

import numpy as np

class PCA:

    def __init__(self, n_components):
        assert n_components >= 1, "n_components must be valid"
        self.n_components = n_components
        self.components_ = None

    def __repr__(self):
        return "PCA(n_components=%d)" % self.n_components

    def fit(self, X, eta=0.01, n_iters=1e4):
        assert self.n_components <= X.shape[1],\
            "n_components must not greater than feature number of X"

        def demean(X):
            return X - np.mean(X, axis=0)

        def f(w, X):
            return np.sum(X.dot(w)**2) / len(X)

        def df(w, X):
            return X.T.dot(X.dot(w)) * 2. / len(X)

        def direction(w):
            return w / np.linalg.norm(w)

        def first_components(X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
            w = direction(initial_w)
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = df(w, X)
                last_w = w
                w = w + eta * gradient
                w = direction(w)
                if(abs(f(w,X) - f(last_w,X)) < epsilon):
                    break

                cur_iter += 1
            return w

        X_pca = demean(X)
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
        for i in range(self.n_components):
            initial_w = np.random.random(X_pca.shape[1])
            w = first_components(X_pca, initial_w, eta, n_iters)
            self.components_[i] = w
            X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w
        return self

    def transform(self, X):
        assert self.components_ is not None, "must fit before transform"
        assert X.shape[1] == self.components_.shape[1]

        return X.dot(self.components_.T)

    def inverse_transform(self, X):
        assert self.components_ is not None, "must fit before transform"
        assert X.shape[1] == self.components_.shape[0]

        return X.dot(self.components_)

pca = PCA(n_components=2)
pca.fit(X)

PCA(n_components=2)

pca.components_

array([[ 0.77871582, 0.62737682], [-0.62737329, 0.77871866]])

pca = PCA(n_components=1)
pca.fit(X)

PCA(n_components=1)

X_reduction = pca.transform(X)
X_reduction.shape

(100, 1)

X_restore = pca.inverse_transform(X_reduction)
X_restore.shape

(100, 2)

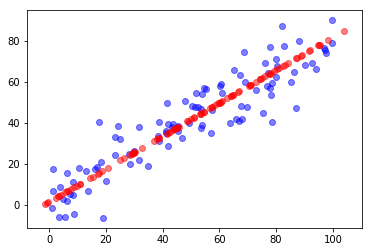
plt.scatter(X[:,0], X[:,1], color='b', alpha=0.5)
plt.scatter(X_restore[:,0], X_restore[:,1], color='r', alpha=0.5)
plt.show()

png

scikit-learn 中的 PCA

from sklearn.decomposition import PCA as SKPCA

skpca = SKPCA(n_components=1)
skpca.fit(X)

PCA(copy=True, iterated_power=’auto’, n_components=1, random_state=None, svd_solver=’auto’, tol=0.0, whiten=False)

skpca.components_

array([[0.77871588, 0.62737674]])

X_SKReduction = skpca.transform(X)
X_SKReduction.shape

(100, 1)

X_SKRestore = skpca.inverse_transform(X_SKReduction)
X_SKRestore.shape

(100, 2)

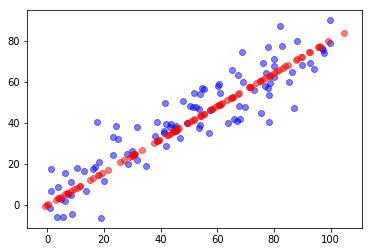
plt.scatter(X[:,0], X[:,1], color='b', alpha=0.5)
plt.scatter(X_SKRestore[:,0], X_SKRestore[:,1], color='r', alpha=0.5)
plt.show()

png