信息熵

熵在信息论中代表

随机变量不确定的度量。

• 熵越大，数据的不确定性越高
• 熵越小，数据的不确定性越低

$p_i$代表第i类数据的占比

比如${\frac{1}{3},\frac{1}{3},\frac{1}{3}}$

在二分类问题中

import numpy as np
import matplotlib.pyplot as plt

def entropy(p):
    return -p * np.log(p) - (1 - p) * np.log(1 - p)

x = np.linspace(0.01, 0.99, 200)
plt.plot(x, entropy(x))
plt.show()

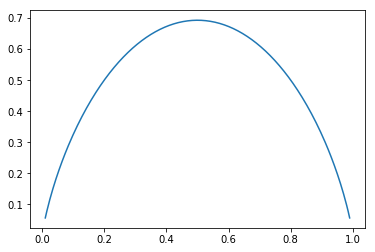
由上图，二分类问题中，当数据各占一半时，信息熵最大，数据的不确定行最大，因为两类数据数量是一样的。

这样一个结论也是可以拓展到多分类问题上。

在决策树的问题时，基于信息熵划分只需要划分后每个节点上的信息熵降低。