逻辑回归

• 解决分类问题
• 将样本的特征和样本发生的概率联系起来，概率是一个数

\[\hat{p} = f(x) \qquad \hat{y} = \begin{cases} 1,\quad \hat{p} \geq 0.5 \\\\ 0,\quad \hat{p} < 0.5 \end{cases}\]

逻辑回归可以看做回归算法，也可以看做是分类算法

通常作为分类算法，只可以解决二分类问题

---

线性回归中$\hat{y}=f(x)$ → $\hat{y} = \theta^T \cdot x_b$

其中值域为：(-infinity， +infinity)

而概率的值域为[0, 1]

则$\hat{p} = \sigma(\theta^T \cdot x_b)$

Sigmoid 函数

\[\hat{p} = \sigma(\theta^T \cdot x_b)\] \[\sigma(t) = \frac{1}{1 + e^{-t}}\]

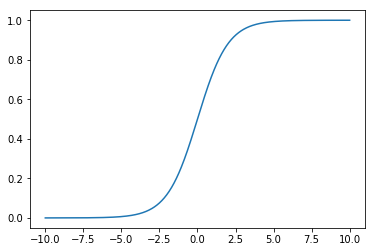
sigmoid函数$\sigma(t) = \frac{1}{1 + e^{-t}}$具有以下性质

• 值域为(0, 1)
• t > 0,p > 0.5
• t < 0,p < 0.5

则，我们可以推出逻辑回归公式

\[\hat{p }= \sigma(\theta^T \cdot x_b) = \frac{1}{1 + e^{-\theta^T \cdot x_b}}\] \[\hat{y} = \begin{cases} 1,\quad \hat{p} \geq 0.5 \\\\ 0,\quad \hat{p} < 0.5 \end{cases}\]

问题：

对于给定的样本数据集X，y，我们如何找到参数theta，使得使用这样的方式，可以最大成度获得样本数据集X，对应的分类输出y？