<-- home

Introduction Of Pca

April 11, 2019

主成分分析（Principal Component Analysis）

  • 不仅应用于机器学习，统计学常用
  • 一个非监督的机器学习算法
  • 主要用于数据降维
  • 通过降维可以发现更便于人类理解的特征
  • 其他应用：可视化；去噪
import numpy as np
import matplotlib.pyplot as plt

X = [
    [1, 2, 3, 4, 5],
    [1.3 , 1.5, 2.5, 4.8, 5.2]
]

plt.scatter(X[0], X[1])
plt.axis([0, 6 ,0, 6])
plt.show()

png

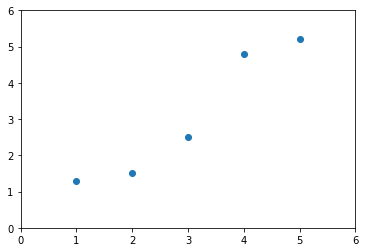
降维

plt.scatter(X[0], np.zeros(len(X[1])))
plt.axis([0, 6 ,0, 6])
plt.show()

png

plt.scatter(np.zeros(len(X[0])), X[1])
plt.axis([0, 6 ,0, 6])
plt.show()

png

以上两种为忽略其中某个特征的降维方法，即投射到两个特征轴的某一个轴

plt.scatter(X[0], X[1])
plt.plot(X[0], X[0])
plt.axis([0, 6 ,0, 6])
plt.show()

png

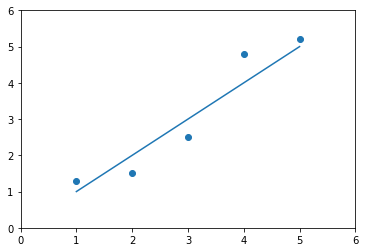
也可以将样本点投射到上述特征轴上，此时，每个样本点在特征空间的距离比较大，我们可以寻找一条线，使得每个样本点在特征空间距离最大，从而与原样本点之间的距离差距更好，样本间的区分度更大，并且，即可以求方差的最大化来找到这条线

PCA 推导

  1. 将样本均值归为0（demean）
plt.scatter(X[0] - np.mean(X[0]), X[1] - np.mean(X[1]))
plt.plot(X[0] - np.mean(X[0]) , X[0]- np.mean(X[0]))
plt.axis([-3, 3 ,-3, 3])
plt.show()

png

\[Var(x) = \frac{1}{m}\sum_{i=1}^m(x_i - \bar{x})^2\]

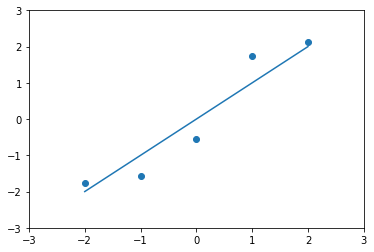
经过demean

\[\bar{x} = 0\] \[Var(x) = \frac{1}{m}\sum_{i=1}^m x_i^2\]

对所有的样本进行demean操作

我们想要求一个轴的方向w = (w1, w2)

使得我们的所有样本映射到w以后，有

\[Var(X_{project}) = \frac{1}{m}\sum_{i=1}^m||X_{project}^{(i)} - \bar{X}_{project}||^2\] \[\bar{X}_{project} = 0\] \[Var(X_{project}) = \frac{1}{m}\sum_{i=1}^m||X_{project}^{(i)}||^2\]

最大

png

则目标：求w使得

\[Var(X_{project}) = \frac{1}{m}\sum_{i=1}^m(X^{(i)} \cdot w)^2\]

最大

一个目标函数的最优化问题，使用梯度上升法解决

和线性回归的差异

  • 在坐标轴中y轴是特征而不是输出标记