支撑向量机 SVM（Support Vector Machine）

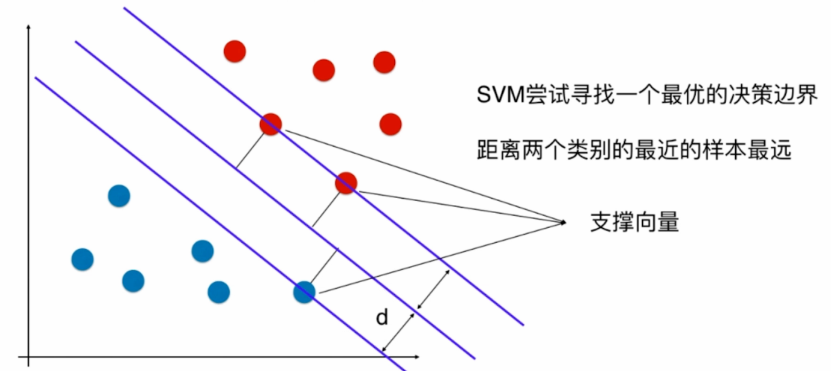
我们称两条经过支撑向量的直线之间的距离为margin，显然margin = 2d

SVM要最大化margin

Hard Margin SVM

解决的是线性可分问题，也就是我们能找到决策边界没有错误的对样本进行了划分和并存在margin

Soft Margin SVM

解决线性不可分的问题，可以改进Hard Margin SVM

x形式化表达

SVM要最大化margin

margin = 2d

SVM要最大化d

点到直线的距离：

(x, y)到Ax + By + C = 0的距离

\[\frac{|Ax + By + C|}{\sqrt{A^2 + B^2}}\]

拓展到n维空间$\theta^Tx_b=0 \Rightarrow w^Tx+b=0$

\[\frac{|w^Tx+b|}{||w||} \quad ||w|| = \sqrt{w_1^2 + w_2^2 + \dots + w_n^2}\]

带入到SVM(把两类中一类叫1，另一类叫-1)

\[\frac{|w^Tx+b|}{||w||} \geq d\] \[\begin{cases} \frac{w^Tx^{(i)}+b}{||w||} \geq d,\qquad \forall y^{(i)} = 1 \\\\ \frac{w^Tx^{(i)}+b}{||w||} \leq -d,\quad \forall y^{(i)} = -1 \end{cases}\]

将d移动到左边（d大于0）

\[\begin{cases} \frac{w^Tx^{(i)}+b}{||w||d} \geq 1,\qquad \forall y^{(i)} = 1 \\\\ \frac{w^Tx^{(i)}+b}{||w||d} \leq -1,\quad \forall y^{(i)} = -1 \end{cases}\]

此时分母为一个数字，将 $w^T$ 和 b 除以分母得到

\[\begin{cases} w_d^Tx^{(i)}+b_d \geq 1,\qquad \forall y^{(i)} = 1 \\\\ w_d^Tx^{(i)}+b_d \leq -1,\quad \forall y^{(i)} = -1 \end{cases}\]

此时我们得到三根线的方程，从上到下依次为

\[w_d^Tx+b_d = 1\] \[w_d^Tx+b_d = 0\] \[w_d^Tx+b_d = -1\]

为了方便书写我们把 $w_d$ 称为 $w$，$b_d$ 称为 $b$，注意此时的 w 和 b 和一开始推算时已经不一样了

\[w^Tx+b = 1\] \[w^Tx+b = 0\] \[w^Tx+b = -1\] \[\begin{cases} w^Tx^{(i)}+b \geq 1,\qquad \forall y^{(i)} = 1 \\\\ w^Tx^{(i)}+b \leq -1,\quad \forall y^{(i)} = -1 \end{cases}\]

得到

\[y^{(i)}(w^Tx^{(i)} + b) \geq 1\]

我们的目标是最大化d

对于任意支撑向量x

\[max\frac{|w^Tx + b|}{||w||} \Rightarrow max\frac{1}{||w||} \Rightarrow min||w||\]

通常为了方便求导我们会求解

\[min\frac{1}{2}||w||^2\]

所以，我们最终的结果是：在满足$y^{(i)}(w^Tx^{(i)} + b) \geq 1$的前提下$min\frac{1}{2}

w

^2$

这是一个有条件最优化问题