Over Fitting And Under Fitting
April 21, 2019
过拟合和欠拟合
欠拟合:
算法所训练的模型不能完整的表述数据关系
过拟合:
算法所训练的模型过多的表达了数据间的噪音关系
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()
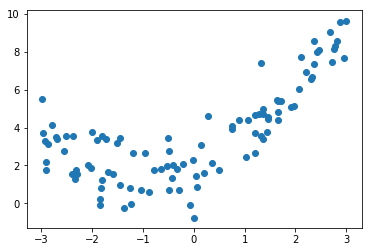
使用线性回归
使用线性回归拟合,并求score和MSE
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
lin_reg.score(X, y)
0.4953707811865009
from sklearn.metrics import mean_squared_error
mean_squared_error(y, y_predict)
3.0750025765636577
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
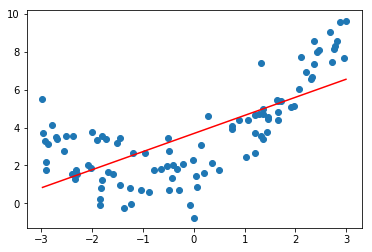
使用多项式回归
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
def PolynomialRegression(degree):
return Pipeline([
("poly", PolynomialFeatures(degree)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
poly_reg = PolynomialRegression(2)
poly_reg.fit(X, y)
y_predict_poly = poly_reg.predict(X)
poly_reg.score(X, y)
0.8196892855998191
mean_squared_error(y, y_predict_poly)
1.0987392142417856
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict_poly[np.argsort(x)], color='r')
plt.show()
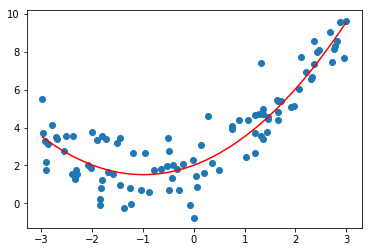
多种 degree 值的多项式回归
poly10_reg = PolynomialRegression(10)
poly10_reg.fit(X, y)
y_predict_poly10 = poly10_reg.predict(X)
poly10_reg.score(X, y)
0.827548782744373
mean_squared_error(y, y_predict_poly10)
1.0508466763764148
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict_poly10[np.argsort(x)], color='r')
plt.show()
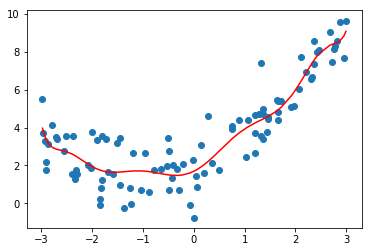
poly100_reg = PolynomialRegression(100)
poly100_reg.fit(X, y)
y_predict_poly100 = poly100_reg.predict(X)
poly100_reg.score(X, y)
0.8871657661853413
mean_squared_error(y, y_predict_poly100)
0.6875653386073417
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict_poly100[np.argsort(x)], color='r')
plt.show()
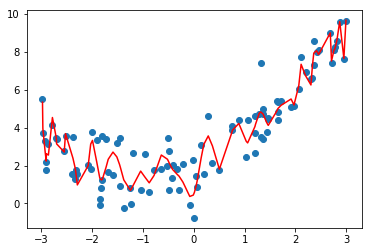
总结
可以看到:
-
当使用线性回归拟合数据时,太过简单不能很好的反应数据的分布,此时处于欠拟合状态,score比较低,MSE比较大
-
当使用degree=2时的多项式回归拟合数据时,能够比较好的反应数据的分布状态,score比较大,MSE比较小
-
当使用degree=10或者100时的多项式回归拟合数据时,得到的结果过于复杂,虽然score进一步增大,MSE进一步减小,但是对于未知的带预测样本可能不能做到很好的预测,此时处于过拟合状态