Precision Recall Tradeoff
May 21, 2019
Precision-Recall 的平衡
- 两个指标同时更加的大有时候是做不到的
- 两个指标互相矛盾
logistic regression 决策边界:$\theta^T \cdot x_b = threshold$
此时threshold是引入的一个超参数,使我们可以平移决策边界
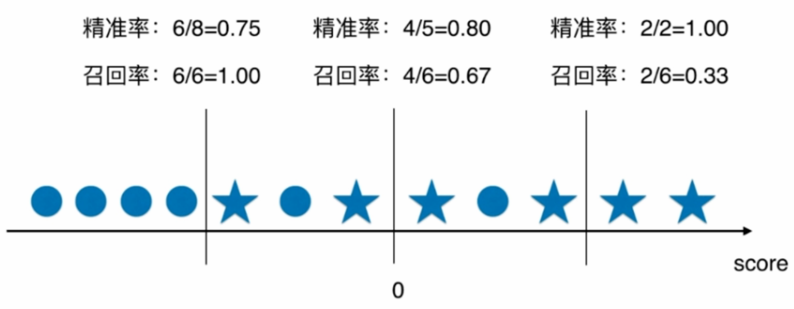
我们改变 threshold 来看看 Precision-Recall 情况
import numpy as np
from sklearn import datasets
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target == 9] = 1
y[digits.target != 9] = 0
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
y_predict = log_reg.predict(X_test)
from sklearn.metrics import f1_score
f1_score(y_test, y_predict)
0.8674698795180723
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_predict)
array([[403, 2], [ 9, 36]], dtype=int64)
from sklearn.metrics import precision_score
precision_score(y_test, y_predict)
0.9473684210526315
from sklearn.metrics import recall_score
recall_score(y_test, y_predict)
0.8
调整 threshold = 5
log_reg.decision_function(X_test)[:10]
array([-22.05700117, -33.02940957, -16.21334087, -80.3791447 , -48.25125396, -24.54005629, -44.39168773, -25.04292757, -0.97829292, -19.7174399 ])
y_predict[:10]
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
decision_scores = log_reg.decision_function(X_test)
np.min(decision_scores)
-85.68608522646575
np.max(decision_scores)
19.8895858799022
y_predict5 = np.array(decision_scores >= 5, dtype=int)
confusion_matrix(y_test, y_predict5)
array([[404, 1], [ 21, 24]], dtype=int64)
precision_score(y_test, y_predict5)
0.96
recall_score(y_test, y_predict5)
0.5333333333333333
调整 threshold = -5
y_predict_5 = np.array(decision_scores >= -5, dtype=int)
confusion_matrix(y_test, y_predict_5)
array([[390, 15], [ 5, 40]], dtype=int64)
precision_score(y_test, y_predict_5)
0.7272727272727273
recall_score(y_test, y_predict_5)
0.8888888888888888