Regularization
April 26, 2019
模型正则化
模型正则化:限制参数的大小
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
过拟合
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
lin_reg = LinearRegression()
def PolynomialRegression(degree):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", lin_reg)
])
from sklearn.metrics import mean_squared_error
poly100_reg = PolynomialRegression(100)
poly100_reg.fit(X, y)
y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)
0.3754848827875088
x_plot = np.linspace(-3, 3 , num=100).reshape(-1, 1)
y_plot = poly100_reg.predict(x_plot)
plt.scatter(x, y)
plt.plot(x_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 10])
plt.show()
lin_reg.coef_
array([ 1.38631499e+13, -1.25544614e+00, 1.56026168e+02, 1.68069375e+03,
-1.68601016e+04, -1.68272359e+05, 7.71064706e+05, 7.23090534e+06,
-1.91996283e+07, -1.74354719e+08, 2.94974315e+08, 2.67388186e+09,
-2.99793818e+09, -2.79560169e+10, 2.09075833e+10, 2.07407006e+11,
-1.01035202e+11, -1.11497852e+12, 3.30270224e+11, 4.36549129e+12,
-6.59203504e+11, -1.22918782e+13, 4.49650719e+11, 2.38651138e+13,
1.37728519e+12, -2.84079880e+13, -4.08949174e+12, 1.19668495e+13,
3.49365070e+12, 1.56684236e+13, 1.92292454e+12, -1.72710909e+13,
-3.90708216e+12, -1.10171333e+13, -2.28767095e+12, 1.50569286e+13,
3.46634225e+12, 1.31064858e+13, 4.25862934e+12, -8.28344845e+12,
-1.52192116e+12, -1.56818437e+13, -5.94812160e+12, -3.53224842e+12,
-1.58040014e+12, 1.16427502e+13, 2.10690938e+12, 1.42875218e+13,
6.62702778e+12, 6.94354739e+11, 2.64446129e+12, -1.09551649e+13,
-3.19269432e+12, -1.38208446e+13, -6.05181353e+12, -1.68263836e+12,
-4.15126552e+12, 5.89280332e+12, -8.50809224e+11, 1.26899958e+13,
6.72112973e+12, 7.01890681e+12, 6.73979114e+12, 5.88869977e+11,
3.65608733e+12, -8.82831561e+12, -3.00647443e+12, -1.03896384e+13,
-5.78071241e+12, -6.80141970e+12, -7.51551904e+12, 4.19132890e+11,
-3.72436213e+12, 7.67422420e+12, 2.34177354e+12, 1.13824834e+13,
6.34139485e+12, 7.08366721e+12, 9.45084773e+12, -1.53316495e+12,
4.21497111e+12, -7.77986203e+12, -2.34938942e+12, -1.00780275e+13,
-7.44948260e+12, -6.36492407e+12, -8.71902608e+12, 2.42418274e+12,
-6.94476956e+12, 9.68478575e+12, 4.17345899e+12, 6.93957780e+12,
1.24289620e+13, 1.40611026e+12, 9.20306220e+12, -7.18328074e+12,
-3.46422073e+12, -6.01580879e+12, -1.81228992e+13, 4.99312135e+12,
9.45158780e+12])
可以看到过拟合的时候系数值会很大
正则化
目标:使
\[\sum_{i=1}^m(y^{(i)} - \theta_0 - \theta_1X_1^{(i)} - \theta_2X_2^{(i)} - \ldots - \theta_nX_n^{(i)})^2\]尽可能小,即
目标:使
\[J(\theta) = MSE(y, \hat{y};\theta)\]尽可能小
加入模型正则化
目标:使
\[J(\theta) = MSE(y, \hat{y};\theta) + \alpha\frac{1}{2}\sum_{i=1}^n\theta_i^2\]尽可能小
- 可以看到模型正则化时,不需要考虑theta0,因为theta0是截距,不影响模型的陡峭程度
- 式子里的二分之一是为了求导后计算方便
- alpha是一个新得超参数,表示正则化时系数的权重,为0时不进行正则化
我们称这种模型正则化为岭回归
岭回归 Ridge Regression
目标:使
\[J(\theta) = MSE(y, \hat{y};\theta) + \alpha\frac{1}{2}\sum_{i=1}^n\theta_i^2\]尽可能小
过拟合
from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
poly20_reg = PolynomialRegression(degree=20)
poly20_reg.fit(X_train, y_train)
y20_predict = poly20_reg.predict(X_test)
mean_squared_error(y_test, y20_predict)
167.94010860867127
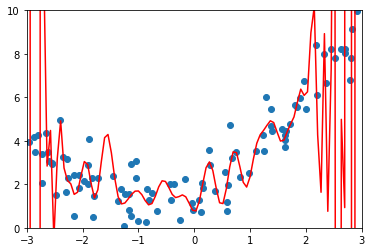
y20_plot = poly20_reg.predict(x_plot)
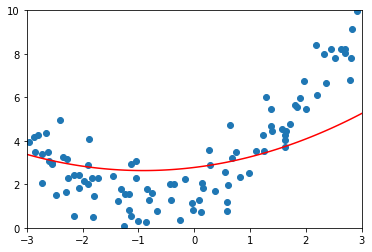
plt.scatter(x, y)
plt.plot(x_plot[:,0], y20_plot, color='r')
plt.axis([-3, 3, 0, 10])
plt.show()
def plot_model(model):
x_plot = np.linspace(-3, 3 , num=100).reshape(-1, 1)
y_plot = model.predict(x_plot)
plt.scatter(x, y)
plt.plot(x_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 10])
plt.show()
岭回归
from sklearn.linear_model import Ridge
def RidgeRegression(degree, alpha):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("ridge_reg", Ridge(alpha=alpha))
])
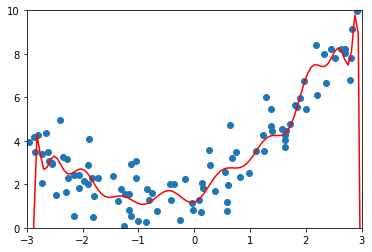
ridge00001_reg = RidgeRegression(20, 0.0001)
ridge00001_reg.fit(X_train, y_train)
y00001_ridge_predict = ridge00001_reg.predict(X_test)
mean_squared_error(y_test, y00001_ridge_predict)
1.3233214212703919
plot_model(ridge00001_reg)
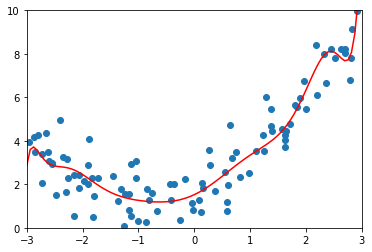
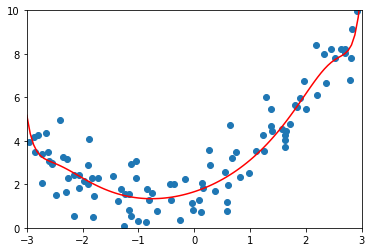
ridge1_reg = RidgeRegression(20, 1)
ridge1_reg.fit(X_train, y_train)
y1_ridge_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test, y1_ridge_predict)
1.1805874402435317
plot_model(ridge1_reg)
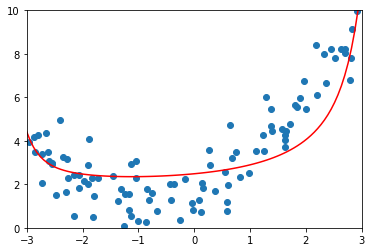
ridge100_reg = RidgeRegression(20, 100)
ridge100_reg.fit(X_train, y_train)
y100_ridge_predict = ridge100_reg.predict(X_test)
mean_squared_error(y_test, y100_ridge_predict)
2.183462033618558
plot_model(ridge100_reg)
LASSO Regression
目标:使
\[J(\theta) = MSE(y,\hat{y};\theta) + \alpha\sum_{i=1}^n|\theta_i|\]尽可能小
LASSO = Least Absolute Shrinkage and Selection Operator Regression
from sklearn.linear_model import Lasso
def LASSORegression(degree, alpha):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lasso_reg", Lasso(alpha=alpha))
])
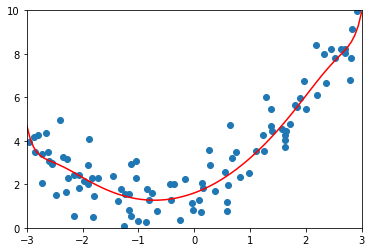
lasso001_reg = LASSORegression(20, 0.01)
lasso001_reg.fit(X_train, y_train)
y_lasso001_predict = lasso001_reg.predict(X_test)
mean_squared_error(y_test, y_lasso001_predict)
1.1495572039164723
plot_model(lasso001_reg)
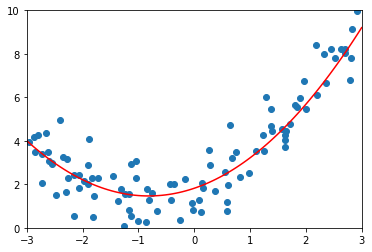
lasso01_reg = LASSORegression(20, 0.1)
lasso01_reg.fit(X_train, y_train)
y_lasso01_predict = lasso01_reg.predict(X_test)
mean_squared_error(y_test, y_lasso01_predict)
1.1213911368888516
plot_model(lasso01_reg)
lasso1_reg = LASSORegression(20, 1)
lasso1_reg.fit(X_train, y_train)
y_lasso1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y_lasso1_predict)
3.2428014186765286
plot_model(lasso1_reg)
比较 Ridge 和 LASSO
- LASSO趋向于使得一部分theta值变为0。所以可以作为特征选择用。
- LASSO有时会将有用的特征忽略,所以计算准确度上Ridge更可靠。
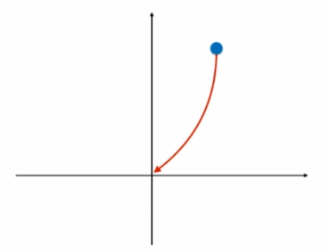
Ridge 梯度下降
当alpha趋于无穷时,梯度
\[\nabla = \alpha\begin{pmatrix} \theta_1 \\\\ \theta_2 \\\\ \ldots \\\\ \theta_n \\\\ \end{pmatrix}\]则theta下降的过程如图
LASSO 梯度下降
当alpha趋于无穷时,梯度
\[\nabla = \alpha\begin{pmatrix} sign(\theta_1) \\\\ sign(\theta_2) \\\\ \ldots \\\\ sign(\theta_n) \\\\ \end{pmatrix}\]其中
\[sign(x) = \begin{cases} -1, x < 0 \\\\ 0, x = 0 \\\\ 1, x>0 \end{cases}\]则theta下降的过程如图