<-- home

Stochastic Gradient Descent

April 8, 2019

随机梯度下降法

批量梯度下降法（Batch Gradient Descent）

对样本中的所有数据进行计算

样本量很大时很耗时

随机梯度下降法（Stochastic Gradient Descent）

  • 抽出一部分样本进行，此时得到的并不是损失函数的梯度，但也代表了一个方向
\[2\cdot \begin{pmatrix} (X_b^{(i)}\theta - y^{(i)}) \cdot X^{(i)}_0 \\\\ (X_b^{(i)}\theta - y^{(i)}) \cdot X^{(i)}_1 \\\\ (X_b^{(i)}\theta - y^{(i)}) \cdot X^{(i)}_2 \\\\ \ldots \\\\ (X_b^{(i)}\theta - y^{(i)}) \cdot X^{(i)}_n \end{pmatrix} = 2 \cdot (X_b^{(i)})^T \cdot (X_b^{(i)}\theta - y^{(i)})\]
  • 学习率η应该递减
\[\eta = \frac{a}{i\_iters + b}\]

这是一种模拟退火的思想，其中a和b是随机梯度下降法的超参数

  • 过程

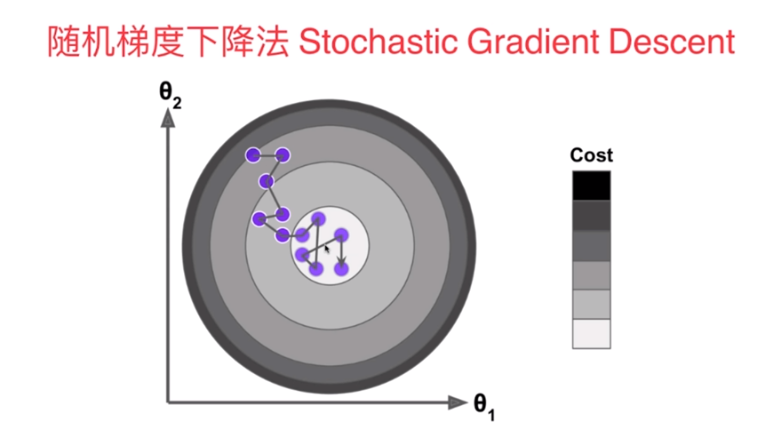
随机梯度下降法

使用梯度下降法和随机梯度下降法对比

梯度下降

import numpy as np
import matplotlib.pyplot as plt

m = 100000

x = np.random.normal(size=m)
X = x.reshape(-1,1)
y = 4. * x + 3. + np.random.normal(0, 3, size=m)

def J(theta, x_b, y):
    try:
        return np.sum((y - x_b.dot(theta)) ** 2) / len(y)
    except:
        return float('inf')

def dJ(theta, x_b, y):
    return x_b.T.dot(x_b.dot(theta) - y) * 2. / len(y)

def gradient_descent(x_b, y, initial_theta, eta, n_iters=10000, epsilon=1e-8):
    theta = initial_theta
    i_iter = 0
    while i_iter < n_iters:
        gradient = dJ(theta, x_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        i_iter = i_iter + 1
        if(abs(J(theta, x_b, y) - J(last_theta, x_b, y)) < epsilon):
            break
    return theta

%%time
X_b = np.hstack([np.ones((len(x),1)), X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)

Wall time: 678 ms

theta

array([2.99357905, 4.00121984])

随机梯度下降

def dJ_sgd(theta, x_b_i, y_i):
    return x_b_i.T.dot(x_b_i.dot(theta) - y_i) * 2.

def sgd(x_b, y, initial_theta, n_iters=10000):
    t0 = 5
    t1 = 50
    def learn_rate(t):
        return t0 / (t + t1)
    theta = initial_theta

    for cur_iters in range(n_iters):
        rand_i = np.random.randint(len(x_b))
        gradient = dJ_sgd(theta, x_b[rand_i], y[rand_i])
        theta = theta - learn_rate(cur_iters) * gradient

    return theta

%%time
X_b = np.hstack([np.ones((len(x),1)), X])
initial_theta = np.zeros(X_b.shape[1])
theta = sgd(X_b, y, initial_theta, n_iters=len(X_b) // 3)

Wall time: 229 ms

theta

array([3.05087812, 3.96798923])

使用我们自己封装SGD

%run ../LinearRegression/LinearRegression.py

%run ../util/model_selection.py

X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

lr1 = LinearRegression()
lr1.fit_sgd(X_train, y_train, n_iters=2)

LinearRegression()

lr1.coef_

array([3.99577204])

lr1.interception_

2.990127765808477

lr1.score(X_test, y_test)

0.6416976315427425

使用真实数据

from sklearn import datasets

boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]

X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

from sklearn.preprocessing import StandardScaler
std = StandardScaler()
std.fit(X_train)
X_train_std = std.transform(X_train)
X_test_std = std.transform(X_test)

lin_reg = LinearRegression()
%time lin_reg.fit_sgd(X_train_std, y_train, n_iters=2)
lin_reg.score(X_test_std, y_test)

Wall time: 12 ms

0.7923329555425149

%time lin_reg.fit_sgd(X_train_std, y_train, n_iters=50)
lin_reg.score(X_test_std, y_test)

Wall time: 124 ms

0.8132440489440969

%time lin_reg.fit_sgd(X_train_std, y_train, n_iters=100)
lin_reg.score(X_test_std, y_test)

Wall time: 166 ms

0.8131685005929717

scikit-learn 中的 SGD

from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor(max_iter=5)
%time sgd_reg.fit(X_train_std, y_train)
sgd_reg.score(X_test_std, y_test)

Wall time: 1e+03 µs

0.8047845970157302

sgd_reg = SGDRegressor(max_iter=100)
%time sgd_reg.fit(X_train_std, y_train)
sgd_reg.score(X_test_std, y_test)

Wall time: 16 ms

0.8132804060803719