<-- home

Use Gradient Ascent To Solve Pca

April 12, 2019

梯度上升法解决主成分分析问题

目标：求w，使得

\[f(X) = \frac{1}{m}\sum_{i=1}^m(X_1^{(i)}w_1 + X_2^{(i)}w_2 + \ldots + X_n^{(i)}w_n)^2\]

最大

为了使用梯度上升法，求梯度：

\[\nabla f = \begin{pmatrix} \frac{\partial f}{\partial w_1} \\\\ \frac{\partial f}{\partial w_2} \\\\ \vdots \\\\ \frac{\partial f}{\partial w_n} \\\\ \end{pmatrix} = \frac{2}{m} \begin{pmatrix} \sum_{i=1}^m(X_1^{(i)}w_1 + X_2^{(i)}w_2 + \ldots + X_n^{(i)}w_n)X_1^{(i)} \\\\ \sum_{i=1}^m(X_1^{(i)}w_1 + X_2^{(i)}w_2 + \ldots + X_n^{(i)}w_n)X_2^{(i)} \\\\ \vdots \\\\ \sum_{i=1}^m(X_1^{(i)}w_1 + X_2^{(i)}w_2 + \ldots + X_n^{(i)}w_n)X_n^{(i)} \\\\ \end{pmatrix} = \begin{pmatrix} \sum_{i=1}^m(X^{(i)}w)X_1^{(i)} \\\\ \sum_{i=1}^m(X^{(i)}w)X_2^{(i)} \\\\ \vdots \\\\ \sum_{i=1}^m(X^{(i)}w)X_n^{(i)} \\\\ \end{pmatrix}\] \[\nabla f = \frac{2}{m} \cdot X^T (Xw)\]

使用梯度上升法求解主成分分析

import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100,2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)

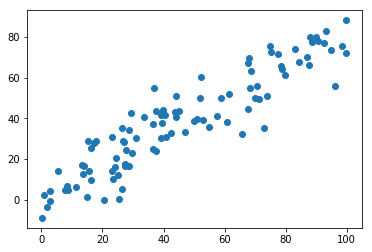
plt.scatter(X[:,0], X[:,1])
plt.show()

png

demean

def demean(X):
    return X - np.mean(X, axis=0)

X_demean = demean(X)
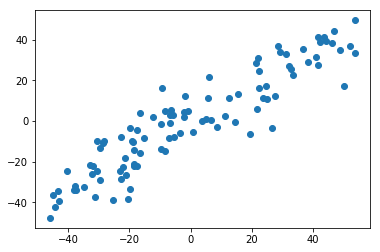
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.show()

png

def f(w, X):
    return np.sum(X.dot(w)**2) / len(X)

def df_math(w, X):
    return X.T.dot(X.dot(w)) * 2. / len(X)

def df_debug(w, X, epsilon=0.0001):
    res = np.empty(len(w))
    for i in range(len(w)):
        w_1 = w.copy()
        w_1[i] += epsilon
        w_2 = w.copy()
        w_2[i] -= epsilon
        res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
    return res

def direction(w):
    return w / np.linalg.norm(w)
def gradient_ascent(df, x, initial_w, eta, n_iters=1e4, epsilon=1e-8):
    w = direction(initial_w)
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = df(w, x)
        last_w = w
        w = w + eta * gradient
        w = direction(w) # 注意1： 每次求一个单位方向
        if(abs(f(w,x) - f(last_w,x)) < epsilon):
            break

        cur_iter += 1
    return w

initial_w = np.random.random(X.shape[1]) # 注意2： 不能用0向量开始
initial_w

array([0.5430665 , 0.35803945])

eta = 0.001
# 注意3 不能使用StandardScaler标准化数据
gradient_ascent(df_debug, X_demean, initial_w, eta)

array([0.76341556, 0.64590764])

gradient_ascent(df_math, X_demean, initial_w, eta)

array([0.76341556, 0.64590764])

w = gradient_ascent(df_math, X_demean, initial_w, eta)
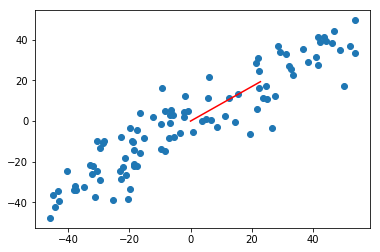
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.plot([0, w[0] * 30], [0, w[1] * 30], color='r')
plt.show()

png

求前 n 个主成分

求出第一主成分后，如何求出下一个主成分？

  • 数据进行改变，将数据在第一个主成分上的分量去掉
\[X^{(i)} \cdot w = ||X_{project}^{(i)}||\] \[X_{project}^{(i)} = ||X_{project}^{(i)} \cdot w||\] \[X^{`(i)} = X^{(i)} - X_{project}^{(i)}\]
  • 在新数据上求第一主成分
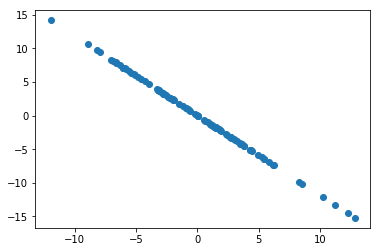
X2 = X_demean - X_demean.dot(w).reshape(-1,1) * w
plt.scatter(X2[:,0],X2[:,1])
plt.show()

png

w2 = gradient_ascent(df_math,X2,initial_w,eta)

w2

array([ 0.64592913, -0.76339738])

w.dot(w2)

2.8141611612908513e-05

def first_n_components(n, X, eta=0.01, n_iters=1e4,epsilon=1e-8):
    X_pca = X.copy()
    X_pca = demean(X_pca)
    res = []
    for i in range(n):
        initial_w = np.random.random(X_pca.shape[1])
        w = gradient_ascent(df_math, X_pca, initial_w, eta)
        res.append(w)

        X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w

    return res

first_n_components(2, X)

[array([0.76341501, 0.64590829]), array([-0.64590508, 0.76341773])]